Problem link: https://codeforces.com/contest/1621/problem/G
I first started with a simpler subproblem: some properties of all increasing subsequences up until i, more specifically, the number of unique sequences and the sum of the length of them. It’s not hard to see we can solve this by some tree structure. (i.e., if before i, the number of unique sequences ending in v is xv, then the value for ai will become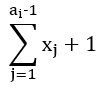 
; if before i, the sum of lengths of sequences ending in v is yv, then the value for ai will become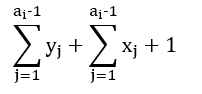 
. And we need discretization to reduce the size of the tree.).
But what about things to the right? Again it’s not hard to see it must have something to do with elements that have nothing greater than them to the right (e.g., [1 2 5] 4 3, both 1 and 2 are “weighted”, but not 5). Let’s call those right maximal. Can we just, for i, find all right maximal to the right of it, that are greater than ai? Unfortunately no, and we can construct a counterexample like [1 6 10] 5, and neither 6 nor 10 is “weighted”.
Even though this immediate thought doesn’t pan out, it does offer some hints. Every sequence that has “unweighted” elements must end on a right maximal. We not only need to consider the right maximal itself, but the maximum to the right of it. And this maximum happens to be the next right maximal. For example, let’s craft a longer sequence to illustrate:
30 100 40 75 86 85 70 90 74 80
From the above observations, we can see:
- For any sequence ending on the right maximal 80, everything is “unweighted”.
- For sequences ending on the right maximal 90, everything between 80 and 90 (89 if you omit the right maximal itself, we will do so for the rest of the article) is “unweighted”.
- Similarly, for sequences ending on 100, everything between 90 and 99 is “unweighted”.
- Actually, for those ending on 80, we can treat as everything between 1 and 79 is “unweighted”.
This is highly suggestive that every element is processed at most once. But how do we find the right subset of elements for each right maximal, while preserving their original order?
With some further analysis, we get this table:
All we need is an upper_bound search (not lower, for elements equal to a previous right maximal) on the array of all right maximal.
Now we can use the exact same tree approach for each segment with the same rank, but this time from right to left. And for every single element, the number of times it’s “unweighted” is the product of the values (number of unique subsequences ending in/starting from element i) from the two trees.
And here we go:
P.S. I’ve been climbing for a while, and recently started to watch IFSC replays. The way climbers (and to a lesser extent myself) tackling problems affects me a lot in programming problem solving. For a moment, while I got stuck on how to handling right maximal, I was projecting myself as climbers under this situation (https://youtu.be/OY0QFlCIpFI?t=9719)
You finish one move at a time, and combined together you solve a bigger problem.