This is a continuation of the last post.
Let’s slightly modify the process: stop when the box becomes empty. And what is the expected number of steps for this process?
The first ball
This is trivial. Whichever other ball is chosen, we always put it back. So until the first ball is chosen (and dropped), for every step, the probability of the first being chosen is 1/N.
And the expected number of steps is simply N.
The next ball and beyond
For the second ball, it’s slightly more complicated, but not by a lot. If it’s not yet chosen, it’s expected to be chosen with probability 1/(N-1) each step, giving N-1 as the expectation. And if it’s already chosen, we don’t have to do anything, giving 0 as the expectation.
And the probability it’s already chose? Well, it’s 1/2. We can pretend ball 3 to N don’t exist, and use the conclusion from the last post. (More on pretending: we can represent the states as nodes in the graph, and when we only consider the state of the first two balls, we only need four nodes. Whenever we pick a ball other than the first two, we can treat it as a self-pointing edge, similar to what we did in the last post. And the ratio between other outgoing edges is what matters.)
So the expected steps to get the first two ball dropped:
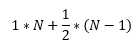
We can generalize this for the i-th ball. To get the probability of that it’s not yet chosen, we can pretend ball (i+1) to N don’t exist,and use the conclusion from last post to get 1/i.
So the overall expectation will be:
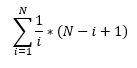
I find this particularly satisfying, as:
- The probability of a ball not yet chosen only depends on the number of balls BEFORE it, and the expected steps to get it chosen only depends on the number of balls AFTER it.
- When dealing with probability, we can always pretend operations that don’t change the state as never happening at all, thus simplifying the calculation.
An afterword on linearity of expectations
The idea is so simple, yet I still find myself failing to internalize it from time to time. Especially the property holds regardless of their joint distribution.
For this particular problem, we can formulate each item in the result as: the expected number of steps to get ball i chosen given the first (i-1) balls are already dropped.
It may sound too trivial, but once we move on to the setting of a tree, as we will do in the next post, the beauty of this property will become more clear.