The actual problem is here on atcoder. I’ll build a solution from the bottom up. So here we go.
Let’s say we have N balls (numbered 1 to N) from a box, and we do the following:
- Take one ball from the box uniformly randomly
- If the ball taken has the smallest number among all the remaining balls, throw it away; otherwise put it back to the box
- If every ball from 1 to N-1 has been taken at least once, stop; otherwise repeat step 1.
And by the time the process is stopped, what’s the probability that the N-th ball has been taken at least once?
First attempt
Since the balls are taken uniformly randomly, is it so that we are equally likely to have either taken or not taken ball N?
Well, a quick simulation suggests otherwise. I’ll leave more rigorous calculations later, but intuitively, it’s similar to the birthday paradox, as the probability of NOT picking ball N at each step multiplies, the overall probability of NOT picking ball N diminishes quickly. (Consider a modified version: uniformly randomly pick a ball for K times and always put the ball back, the probability of ball N NOT picked is ((N-1)/N)^K).
In search of an explanation with the answer
From simulation, it’s obvious the answer is (N-1)/N.
One explanation I came up with: If we change the condition “If the ball taken has the smallest number among all the remaining balls, throw it away; otherwise put it back to the box” to “always put the ball back to the box“, it doesn’t change the the probability of whether the N-th ball get picked at all. (But it does change the value of something else, which is the topic of next post.) Convince yourself: if we pick up ball 1, put it back, and later pick it up again, we can just pretend this step doesn’t happen. Then graphically:
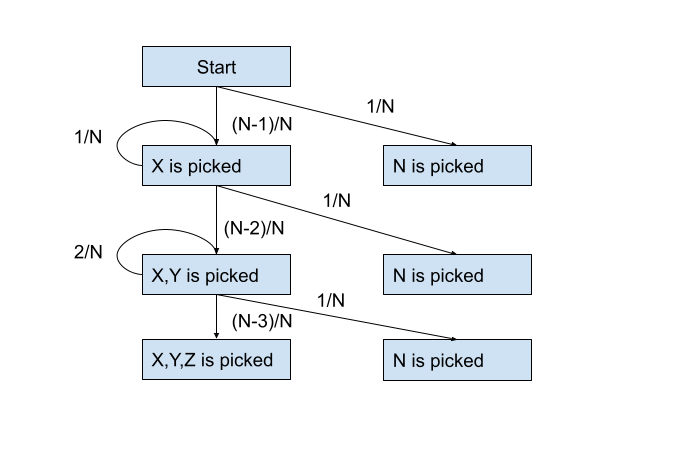
Regardless of the the values on those self-pointing arrows, the ratio on the other two outgoing arrows stay the same, and if we go to infinity, we get the resulting probability.
A failed algebraic approach
I also tried to solve it algebraically or with induction. But to decide the property of the N-th ball, it depends on the (N-1)-th ball, then the property of this pair depends on the (N-2)-th, then the property of this triple depends on the (N-3)-th, etc. The formula just keeps growing.